Para un campo B Negativo

Procedemos ahora de forma completamente análoga a la anterior, pero invirtiendo el sentido en que la intensidad recorre las espiras de las bobinas.

En esta ocasión los datos son:

IB (A)  ERROR DE IB          V (mV)            ERROR DE V           B (mT)            ERROR DE B          

0,00    0,01    -7,1     0,1       9          2         

-0,49   0,01    -3,8     0,1       -45      2         

-1,05   0,01    0,4       0,1       -107    2         

-1,52   0,01    3,9       0,1       -158    3         

-1,99   0,01    7,3       0,1       -210    3         

-2,49   0,01    10,8    0,1       -265    3         

-3,00   0,01    14,4    0,1       -321    3         

-3,53   0,01    17,6    0,1       -379    4         

-4,15   0,01    21,0    0,1       -448    4           

            Y la gráfica:

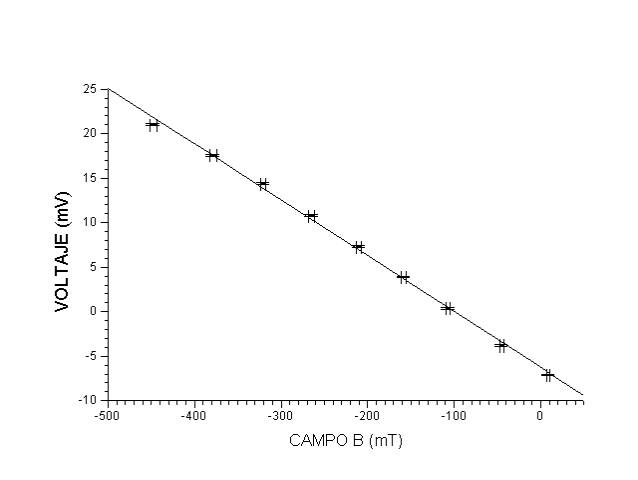
fig. 9

El ajuste da:

Linear Regression for DATA1_B:

Y = A + B * X

Param            Value  sd

A         -6,25265        0,28421

B         -0,06277        0,0011

R  = -0,99893

SD = 0,47834, N = 9

P = 1,3356E-10           

Donde vemos que la pendiente es en esta ocasión -0.063+/-0.001.

Operando igual que en el caso anterior, y fijándonos que esta pendiente es virtualmente la misma que en aquel caso, tenemos, una vez más:

RH = (-6.3+/-0.1)E-3 WmT-1